Batch 2 - Class 102 - Zero Knowledge Proofs
Pre-Class Problem:
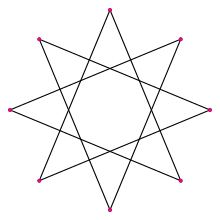
- (Geoffrey: 28) There is an eight pointed star. You must place a penny on one point, and slide it along the line till it reaches another point across. Place seven pennies in this manner.
Attendance: Anisha, Muskaan, Tishyaa, Nandini, Khushi, Arnav, Anishka, Anshi
Class Notes:
Alibaba and Caves: Alibaba knows the secret to open a passage through a cave. You don't believe him and ask him to prove that he knows the secret code.

- Ask kids how to determine if someone knows the secret code?
- Straightforward way is to ask the secret and test it
- What if the prover doesn't want to part with the secret. Can you still know if he knows the secret?
- Yes, the prover goes in through a branch, and comes out of the other
- What if the prover doesn't want you to be able to prove to others that he knows the secret?
- Random repeats of the experiment
- Why cant the observer show others that the prover knows the secret even by taping the whole film?
Zero Knowledge proofs:
These are proofs where the prover can prove the statement without sharing the secret (the "how"), at the same time not allowing the verifier to know anything more than now believing in the proof. Specifically, the verifier should not be able to prove it to others!
Graph Coloring and Google: There is a telecom company which wants to identify a pattern to color a graph with three colors (to identify non-interfering frequency patterns for their cell towers). Google claims that it has a solution.
- If there was no constraint, how would the company ascertain that Google has a solution?
- By asking Google to reveal
- What if Google didn't want to reveal the solution unless it is paid by the Company, and company doesn't want to pay unless it knows that Google has a solution.
- In each try, Google colors the vertices with choice of three colors, and covers the coloring. The company asks for a particular edge to be revealed, and if after multiple tries all edges come clean, then most probably, Google has a solution
- If the company was trying to convince someone else who was not at the site to observe, could it do so?
- No - the company could have colluded with Google
- No - the company could have only shown the successful attempts and edited the others
- Hence this is a Zero Knowledge Proof
Lets run a scam: We need at least 8 kids to do this. I will write a sequence of 3 0s and 1s on a paper and hand it over to kids. Then I will toss a coin in exact same sequence that I had written and given earlier. Kids must stay quiet, other than the fact that if any kid sees the sequence being repeated exactly, and hence is convinced of my prediction capability, they should say "Hail Alok". Voila! in each round I can demonstrate 100% prediction capability to some kid!
- Explain how a fraud investment scheme can work this way
Computing Cheating Instances: Math department of a certain university wants to estimate what percentage of students cheat in an exam. How should it do so?
- What will happen if it just asks the kids?
- What will happen if there is a secret ballot - what if a particular student's name is revealed with her answer?
- How can students be sure that they can answer the question without risk of being caught?
- Some answer honestly, some answer randomly
- Can the department get to know the percentage of students who cheat in this method?
- If a particular student's name and answer is revealed, what do we know about their cheating behavior?
Getting Relatives to Cooperate: I have a set of relatives, say 10 who wouldn't cooperate with each other on anything. I will give them a reward if they cooperate - for example, by putting the reward in a suitcase with a 3-digit combination lock. However, I want them to be able to open the lock only if they cooperate. Can you help me set up a way of doing this?
- What if there are only two relatives?
- What if there are three relatives who need to cooperate?
- What if there are three relatives and I want at least two to cooperate?
- Extrapolate to ten relatives
- If they did collaborate, and I wasn't there to observe them collaborating, could they prove to me that they collaborated?
- Could I in turn convince them that the relatives indeed collaborated?
Homework
The Same Court Time
Basketball is one of the most popular team sports in this summer’s Olympic Games. The game is played with five players from each side on the court at the same time, and is played for four 10-minute quarters. The coach of the Brazil team has decided to give every one of her eight players the same court time. What scheme should she use to ensure this?
- Many ways to solve for this. One easy solution is 12345, 23456, 34567, 45678, 56781, 67812, 78123, 81234
- Another funny one is to forfeit!
- Another one is to have the coach play all through and then give each player two quarters!
References: